Of the most advanced forms of the latter type of geomancy are the sikidy divination of Madagascar and the Bamana divination of Senegal.
Sikidy uses a randomly-generated set of columns of seeds to produce what is known as a mother sikidy. Then, through a set algorithm, 16 columns are generated by combining mother columns using an exclusive-or (XOR) operation.
The sikidy master, known as ombiasy, uses three checks to make sure the algorithm has been carried out correctly.
One check involves what is known as even parity checking of a specific column. The other two checks are based on algebraic logic after establishing the algebraic properties of the columns or combination of columns. One check involves making sure that at least two columns are identical, which will always be true if the algorithm is properly performed.
The other involves what are called "the three inseparables" in which the XOR of three different pairs of columns should produce the same sum.
Each column permutation represents a cardinal direction, and if any particular cast results in all four directions appearing it is known as a sikidy unique. This type of divination is considered particularly auspicious, and ombiasy are said to have secret rules for producing these outcomes.
One might see here similarity with modern computer techniques. Indeed, Leibniz was inspired to write his binary code after studying the binary notation of the I Ching, and also geomancy-inspired works of Raymond Hull, which have their ultimate origin in African systems like Bamana and Sikidy divination.
The boolean logic of Sikidy reminds us also of the work of Boole, while the XOR operation and parity checking were used by Shannon and Hamming respectively who were particularly interested in encryption and network communications.
Even the 16 figures/signs of sikidy and related geomancy forms brings to mind the 16 bit register which heralded the invention of the microprocessor.
Origins
The question of origin and spread of the 16-sign geomancy is quite a matter of controversy. Often it is tied together with similar theories on games/gambling of the type described under the general terms mancala or sungka.
The connection with mancala is not without merit. First of all, there are many cases of divination systems mutating into game or gambling forms, or vice a versa. Chinese chess originally was a form of battlefield divination in which magnetic pieces were cast on to the ground or a divining board. The disposition of the pieces allowed the diviner, according to this system, to predict an outcome or conditions of a future battle.
In the Philippines, the Dado dice divination of the Ayta is now largely, but not entirely, used for gambling purposes. Sungka in the same region is mostly a sedentary past-time, but previously it was also a gambling game. In Bergano's dictionary of Kapampangan, the word sungca could refer to the game, but also to a wager placed on the game.
Mancala and 16-sign geomancy also share a number of morphological and possible genetic features. Both have a strong binary structure.
For example, with sungka-type games having two pieces -- one each in cup 1 and cup 2 -- one can replicate the situation in two moves. The pieces will end up in cup 3 and cup 4. On a 16-cup board, one can move recursively around the board with each cycle ending one cup advanced from the last starting point.
Or one can start with two pieces in one cup and produce the same recursive pattern. In imagery that will become clearer later in this article, we can think of the two pieces in unison as analogous to a New Moon with Sun and Moon together. On the next move, the two will be in separate cups representing the opposition/separation of a Full Moon. And then on the second move, they are back together again. So the first move would represent the bright fortnight, and the second move the dark fortnight.
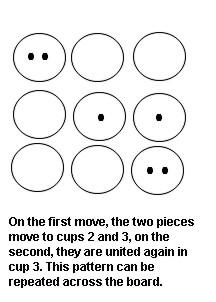
With the 16-cup Sungka-type game, one counts modulo 8 with reference to the opponent's side, and modulo 15 for circling around the whole board.
The cups are also set in opposition to each other to include the "mother" cups in the Sungka game. When one captures pieces in this game it is always from both opposing cups.
Both 16-sign geomancy and mancala-type games also share an emphasis in randomization. In contrast to board games like checkers and chess, it is very difficult to consider many moves in advance of the one at hand. This is one reason why computer scientists have a much harder time programming computers to play mancala as oppossed to chess, where some computers have defeated grandmasters.
In fact, with the more complex mancala games it has been proven that there is no solution to finding total permutations for a signifanct number of advance moves.
This is because unlike chess, where any one move usually effects only the piece involved, or at most two pieces during a capture or castle, a single move in mancala will often change every position on the board.
Because of this randomizing effect, a mancala player usually must face unpredicted and unpredictable situations more often than with games like chess.
In 16-sign geomancy, we have shown also that randomizing is an important feature. In advanced forms like sikidy and bamana divination, the diviner goes through extra procedures to assure a random distribution.
Also the two systems share many morphological similarities. For example, 16-sign geomancy often uses the same cups, pits, seeds, cowries, pebbles, etc. as mancala, and arranged in similar fashion. Both rely mainly on counting methods.
Finally, the geographical distribution of mancala and 16-sign geometry share some important overlapping that does not appear coincidental.
Competing theories
Numerous theories arise as to both the origin and distribution of mancala and 16-sign geomancy either as paired cultural items or as separate events.
P. Townshend and R. Eglash make strong arguments for the African origin of both items. They note that the mathematical systems and cultural milieu of both 16-sign geomancy and mancala are right at home in Africa.
For example, base 2 mathematics defines most tropical African numeration being used even for multiplication and division. The randomization and recursiveness of the two cultural systems also show up pervasively in African weaving and other design-making techniques displaying complex fractal symmetry.
On the other hand, the same systems seem out of place in the Islamic Arab schools of thinking, thus addressing another major theory of origin and diffusion.
Wim van Binsbergen, for example, suggests that mancala originates in the "Fertile Crescent" and was mostly spread through Islamic carriers. However, the maps he shows in support of this contention might surprise many who have studied this subject. It seems that all the early evidence he uses to support the Fertile Crescent is of archaeological nature.
Most of the examples don't even have any precise morphological similarity to modern mancala-type games other than consisting of horizontal surfaces with cup-markings.
Using such methodology, one might mistake konane of ancient Hawai`i with mancala as it often uses pitted boards together with pebbles. However, konane is not primarily a counting game and is similar to Malayan Tjuki (and European draughts, checkers) instead. It may be that these games have some relationship, but one should not be confused for another.
The current distribution of mancala games betrays no bias toward Muslim populations. For example, in India, counting-type games often appear more common and popular in eastern parts of the country and among tribals.
In Africa, these games are highly important elements of the local culture and dispersed often without linguistic or historical evidence of Muslim influence.
Also, van Binsbergen dismisses the Pacific distribution of mancala-type games without giving any supporting evidence for his conclusions.
Tumtum al-Hindi
Turning to 16-sign geomancy, the earliest texts we have for this system are actually European. There are earlier Islamic texts that mention geomancy of some type, but none give details until the work of al-Zenati.
However, the European works themselves are merely translations or translated paraphrasing of Arabic works from Toledo.
Both the Muslim and European writings credit this form of geomancy to one Tumtum al-Hindi. Although the line of descent is sometimes taken back to Idris (Enoch), most works mainly reference Tumtum in explaining the origins of the various facets of 16-sign divination known in Arabic as 'ilm al-raml.
European tradition states that Tumtum learned the art directly from the angel Gabriel.
Now, Tumtum originates from al-Hind, which in this blog we have explained as referring to "Greater India" or "India Major." This generally meant South India starting at Malabar, and further India, or basically all of mainland and insular Southeast Asia.
We should note here an interesting work by Jean-Pierre Grind, that points out the similarity between the figures used in Arabic, and thus also European geomancy, and the 16 tetragrams of Zhu Xi (1130-1200 AD) and Shao Yong (1011-1077).
These appear, or at the least Shao Yong's work appears before the writings of Hugues de Santalla sometime in the 12th century, where we first meet with a detailed description of 'ilm al-raml.
Zhu Xi in particular was interested in I Ching divination so the striking correspondence between the tetragrams and figures cannot be ignored.
However, there still is a great deal of difference between the practical aspects of the I Ching and 'ilm al-raml. The signs used in the latter also seem more similar to the pits or cup signs used in African systems and in mancala-type games.
And what of Tumtum al-Hindi?
There is indeed evidence, as we have dicussed earlier, of some transfer of Chinese knowledge to the Islamic and European worlds at the time in question.
Durng the same period, Prester John of the Indies makes his appearance on Europe's horizon. There was a definite influence also from the "Indies" that gets profuse mention even in the medieval romantic cycles.
Could Tumtum have been a traveler from Hind (India Major) to Madagascar and/or other places in Africa?
If Tumtum did indeed exist, and where ever he came from exactly, it's unlikely he was carrying some fully-formed 16-sign sikidy-like geomancy with him. Such systems are nearly absent from the classic territory of al-Hind (which must be separated from Sind or Zanj, the other two "Indias").
Prototypes
However, Tumtum could have brought ideas that merged with local African thinking to help develop the geomancy that eventually reached North Africa and Europe.
In my other writings, I have theorized that these ideas involved the combination of divination techniques with what is known as electional astrology.
Like many others, I believe that the mancala games were diffused first, but at an earlier time than generally considered. It may be they were part of the package of cultural exchange that began with the opening of the spice trade routes between Africa, South Asia and Southeast Asia. This could explain the concentration of distribution in tropical Africa and the Indian Ocean.
Mancala could have been distributed into the Pacific isles of Micronesia and Papua at the same time as cultural items like betel nut and coconut wine fermentation.
It also seems highly likely to me that mancala was diffused in Africa before the Bantu expansion, which helps explain its presence in inner Africa and in places where it shows little sign of Islamic influence.
Also, I believe the 16-cup Sungka game using a canoe-shaped board is related to the knot divination of the Caroline Islands. Here we find the 16 Bwe spirits consulted in that divination system depicted in the "canoe of destiny."
Knot records were widely used in Southeast and East Asia. There are also records of knot divination.
Miguel de Loarca, for example, writing in 1582 mentions such use among of the natives of the Philippines:
These natives have a method of casting lots with the teeth of a crocodile or of a wild boar. During the ceremony they invoke their gods and their ancestor, and inquire of them as to the result of their wars and their journeys. By knots or loops which they make with cords, they foretell what will happen to them; and they resort to these practices for everything they have to undertake.
--- Relacion de las Yslas Filipinas
The loops mentioned above may refer to string figures or cat's cradles so popular in this region and out into the Pacific. Early observers mention some 400 types of string figures in the Pacific, with 115 in Hawai`i alone. String figures were also used for divination in this region as in the Hawaiian art of kaula.
The 16 Bwe of the Carolines are known as Tilifek, Lipul, Pukenamar, Saupith, Mesauk, Pwainek, Sauya, Lithanwel, Inemain, Inifau, Momo, Inipwai, Laneperen, Lifar, Inoaeman and Toalefailan.
Tilifek is portrayed as sitting on the outrigger of the canoe of destiny, while Inoaeman and Toalefailan sit on the platform. All the others are seated within the canoe.
In various myths of the Bwe, the canoe of destiny comes down from Heaven, and events in the story are often coordinated with successive Full Moons. In one myth, at the end, the Bwe sail back to heaven in the canoe of destiny.
The heavenly connotations are important here because I have suggested that the 16 cups of the Sungka board are related to the lunar fortnights. The two large "mother" cups on each end would represent the New and Full Moons, and the the two rows of seven smaller cups stand for the two weeks in each fortnight.
The actual mean length of the synodic fortnight is 14.765295 days, but in most cultures this would be rounded to the nearest day with the remainder handled by intercalation if necessary.
In the Sungka method of play, one drops cowries or other pieces into each cup and into one's own mother cup, but not into one's opponent's mother cup. Thus, the counting for a full circle around the board is modulo 15, the length of a fortnight.
Electional astrology
In many areas of this region, electional astrology, the choosing of auspicious times for undertakings, is among the most pervasive of predictive systems.
These usually involve either the synodic or sidereal lunar month. In the case of the sidereal month, the conjunction of the Moon with certain stars or asterisms was used to choose good or bad days for various ventures and undertakings.
Also, numerous written divination calendars are found in Sumatra and Borneo, which outline auspicious days, although these often combine outside cultural influences.
At some time, there may have been a desire to combine divination with electional astrology resulting in the creation of a 16-sign system based on the lunar days.
Here then the canoe shape of the Sungka board like the "canoe of destiny" represents the movement of the celestial bodies in heaven.

We can seen something very similar possibly in the Dado dice divination. On four sides of the six-sided dice are representations of constellations important to the Ayta. These stars may have been watched at one time for conjunctions with the Moon in electional astrology.
For divination purposes, each lunar day was associated with particular deities, spirits, significations, etc. and the answer to a query would depend on the disposition of the entire set.
The use of the Sungka board in a simpler fashion for folk divination has continued up until recent times, if not till the present. In this case, Sungka is played in "solitaire" fashion by family diviners with the query answer based on the outcome of the game.
However, at some point the board became more used as a game than a divination device.
Fusion
The idea of lunar signs however continued to be used as, for example, in knot divination.
Eventually these 16 signs may become more abstract and not so much associated with the lunar days (or the associated deities, significations, etc.).
Possibly such a system was taken by Tumtum al-Hindi from some place in al-Hind to Africa.
Here, Tumtum learned African mathematics consulting with local savants. This would include African techniques of randomization and modulo 2 arithmetic.
By fusing these techniques together he developed the sikidy-like forms of divination, or at least the forms that eventually led to `ilm al-raml and European geomancy.
Although the spice trade faciliated cultural exchange, regions from both sides of the Indian Ocean retained their specific cultural tendencies.
Eglash, for example, has categorized the "Eulerian" designs of the Pacific and Southeast Asia as basically Euclidian and algebraic, while African designs are inherently fractal. Also, determinism is an important part of African divination in combination with randomization, but not so important further East.
For example, the strict algorithms and multiple checks, along with the rumored rules for generating sikidy uniques are evidence of the determinism mentioned by Eglash.
In sikidy and 'ilm al-raml, we find these aspects of determinism, algebraic logic, binary logic, electional/time orientation, etc. fused together.
This might explain the legends in Madagascar that attribute the origin of Sikidy to ancestors who came across the sea, which also could ultimately explain the origin of Tumtum al-Hindi as found in Muslim and European texts.
In this sense, the Arabic elements found in Sikidy, and often used to give an Arab origin to this system are better explained as adstrata. The same elements could, however, explain the transmission of the science to the Arabs that eventually led to 'ilm al-raml.
At this time, the Indian Ocean was a very active place with strong competition for control of the trade routes. The Prester John contacts with Europe begin during this period, and also similar approaches with China and India.
Thus, we find the wide diffusion of 16 lunar-based signs starting in the 11th century or so from China to Europe. But strangely, Tumtum's Africanized system never took hold in his supposed homeland of al-Hind.
Regards,
Paul Kekai Manansala
Sacramento
References
Ascher, Maria, Mathematics Elsewhere: An Exploration of Ideas Across Cultures, Princeton University Press, 2002.
Eglash, R. "Fractal Geometry in African Material Culture." Symmetry: Culture and Science, 1995b, Vol 6-1, pp 174-177.
___. "When Math Worlds Collide: Intention and Invention in Ethnomathematics," Science, Technology and Human Values, 22(1), 1997, pp. 79-97.
Selin, Helaine and Ubiratan D'Ambrosio, Mathematics Across Cultures: The History of Non-Western Mathematics, Springer, 2000.
Townshend, P., "Mankala in eastern and southern Africa: A distributional analysis," Azania, 14: 109-138, 1979a.
___, "Games of strategy: A new look at correlates and cross-cultural methods," in: H.B. Schwartzman, ed. Play and culture, New York: West Point, 1979b, pp. 217-225.
___, "Bao (Mankala): The Swahili ethic in African idiom," Paideuma 28: 175-191, 1982.
van Binsbergen, Wim, Board-games and divination in global cultural history, Part 1, http://www.shikanda.net/ancient_models/gen3/mankala/mankala1.htm and Part II, http://www.shikanda.net/ancient_models/gen3/mankala/mankala2.htm, 1999.






