R. Campbell found that some kaikai chants were in fact identical to songs written in the native script known as rongorongo. Experts believe it may be possible to also match up the texts of pata'uta'u string games with the rongorongo of the Easter Island tablets.
Indeed, a number of rongorongo signs closely resemble Easter Island string figures, and bird symbolism was important in both practices.

Rongorongo inscription, Small Santiago Tablet, source: http://www.rongorongo.org
In a similar manner, Chinese tradition tells us that Fu Hsi used knot records that became one of the prototypes for the future Chinese script.
Some extant texts exist showing the depiction of numbers using black and white knots. The black knots represent even numbers, night, cold, water and Earth. The white knows stand for odd numbers, day, warmth and Sun. These knots represented also the principles of yin and yang, and served as models for the trigrams, which were likewise credited to Fu Hsi.
The Hetu or "River Map" of Fu Hsi, and the Luoshu or "Luo River Writing" of Yu the Great, are portrayed as cosmic maps that depict the universe with sets of connected black and white dots representing respectively even and odd numbers.

The top row shows two extant Chinese tablets with even numbers represented by strings of black dots, and odd numbers by strings of white dots. On the second row, the Luo River Writing (L), which Yu the Great found on the back of a turtle emerging from the Luo Shui River. The Hetu, or River Map (R), found by Fu Hsi written on a "dragon-horse" that arose from the Yellow River. In both cases, the black dots stand for yin and even numbers, and the white dots represent yang and odd numbers.
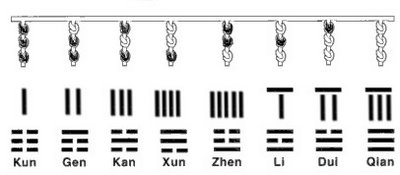
Possible evolution of trigrams from binary knot system using counting stick images. On the top row is a cord of strings with dark knots representing even numbers and yin characteristics, and white knots: odd numbers and yang characteristics. The center row shows the numbers 1-8 using Chinese counting sticks. The image of the counting sticks is used to form the trigrams with the solid lines standing for the white knots and the broken lines for the yin knots.
Interestingly, the numerals used for the numbers 1 to 3 in many ancient scripts appear related to tally sticks or pebbles, shells, beads, etc. used for counting.
The similarity to tally sticks breaks off with the number four in half the scripts involved suggesting that maybe, if there is some relationship between these symbols, that it involves a base-four counting system.
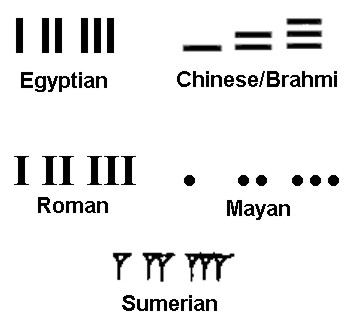
Numerals from 1 to 3 in various ancient scripts
Base-four numeration is scattered here and there all over the world.
The practice of counting items like yams, coconuts, bananas, taro, fish, etc. by fours is rather commonly found in the Pacific both among Papuan and Austronesian peoples.
In Hawai`i, counting by fours is known as kauna and is still used in some fish markets especially for counting the opelu fish. According to tradition, a fisherman could hold four fish by there tails, two in each hand, or four taros in the same way. The kauna method supplements the ancient Proto-Austronesian decimal system.
kauna -- 4
ka'au -- 40
lau -- 400
mano -- 4,000
kini -- 40,000
lehu -- 400,000
J. Przyluski in studying the ganda guti system of numeration among the Mundas believed the origin to stem back to Austro-Asiatic and even to Proto-Austric.
The gandaka system of counting by fours in other Indian languages is thought by many to have been modeled after the ganda guti numeration.
Ganda monetary system
4 kauri (cowries) = 1 ganda
20 ganda = 1 pan (80 kauri)
4 pan = 1 ana
4 ana = 1 kahan
4 kahan = 1 rupee
That the above system used cowries as a form of currency is seen as evidence of its origin among a maritime people.
In the Philippines, counting by fours is found in systems like the measure based on the ganta still used mainly for measuring rice.
Apatan (divided by four)
4 apatan = 1 gahinan (chupa)
4 gahinan = 1 cagitnaan
4 gatang = 1 ganta (8 gahinan/chupas)
There are other four-based systems like that used in Pampanga for measuring spun cotton: 4 cauing = 1 cabid; 10 cabid = 1 tul (40 cauing).
Counting by fours probably originally involved using the four fingers with the thumb used only as a placeholder. Eventually, this involved into a base eight numeration by using both hands.
The Bagua or octogonal arrangement of the trigrams, instituted by Fu Hsi, can indicate the use of base four systems, one with each hand to form a base eight numeration. Thus, the first trigram in this arrangement (seen above) is the polar opposite of the eighth trigram. The second trigram is the opposite of the seventh trigram, and so on.
Knot records
In the 1700s, George Keate wrote of the encounter of Captain Wilson and the king of Palau, Abba Thulle and his son Lee Boo. The king gave Captain Wilson permission to take Lee Boo with him to England and promptly constructed a knot calendar by which he would track the voyage of his son.
Lee Boo also used a series of string records to memorize the name of every ship and country they encountered along the way to England.
Unfortunately as with most early notices of knot records, little information is given on to the precise methods used. However, little bits of information are available here and there from the many cultures that used this type of record-keeping.
In the Ryukyus, a string of knots sent to woodcutters indicated the type of trees to be cut by a leaf inserted in the knot. Knots at certain locations on the string indicated the quantity and dimensions of the timber required. Pawnbrokers on the Ryukyus used knots to record the amount of debts with fractions indicated on subsidiary strings. Different types of knots represented the various months in the payment schedule.
The Santals of India used different colored knots in their census to record the population -- black for adult men, red for adult women, white for boys and yellow for girls.
One of the most detailed accounts was that of a massive tax-recorders cord, nearly a half-mile in length, found by Tyerman and Bennet in Hawai`i in 1822:
The tax-gatherers, though they can neither read nor write, keep very exact accounts of all the articles, of all kinds, collected from the inhabitants throughout the island. This is done principally by one man, and the register is nothing more than a line of cordage from four to five hundred fathoms in length. Distinct portions of this are allotted to the various districts, which are known one from another by knots, loops, and tufts, of different shapes, sizes and colors. Each taxpayer in the district has his part in this string, and the number of dollars, hogs, dogs, pieces of sandal-wood, quantity of taro &c, at which he is rated, is well defined by means of marks, of the above kinds, most ingeniously diversified. It is probable that the famous quippos, or system of knots, whereby the records of the ancient Peruvian empire are said to have been kept, were a similar, and perhaps not much more comprehensive, mode of reckoning dates and associating names with historical events.
On the Marquesas islands in French Polynesia, priests were able to read off their ancestors that were indicated by knots on a string going back to the first man and woman. Referring to a specific knot genealogy discovered by von den Steinen, Cyrus L. Day says:
"...Karl von den Steinen saw a Marquesan knot-genealogy that went back 159 generations or (counting thirty years to a generation) to about 2870 B.C. The Mikado of Japan, he remarks, is a mere parvenu compared with some of the unlettered princelings of the Pacific islands; for the family trees of the Marquesans go back to the earliest colonization of the archipelago, to the gods of Hawaiki (the legendary homeland of the race), and even to the myths of the creation of the universe."
The Marquesan to'o knot records were multi-purpose with one cord pontentially containing genealogies, religious chants, songs and other information.
Symbolic records on totem poles/menhirs, textiles, rafters, tattoos, etc.
The use of symbols to indicate genealogy, heroic accomplishments and the like on ancestral objects like totem poles or the rafters of ancestral houses is found repeatedly throughout the Austronesian and Nusantao region.
As with knot records, interpretation of such symbols was largely a private matter of the recorder or artist and those who were instructed as to their meaning. However, there are also cases of more or less "standardized" symbols that were used for public communication.
The location of the symbols as, for example, the position of tattoo marks on the face of a Maori warrior, often was essential for correct interpretation. In the same sense, the position of drawings on the ridgepole and rafters of the Maori meeting-house, and the position of carved images on the veranda, walls and on support posts, are integral to their meaning. The same symbol in different locations could have different meanings. In this sense, the system was graphic in nature similar to a genealogical tree or a geographical map.
Certainly there could be a relationship between these symbolic systems and the mapping techiques found in the wave piloting stick charts of the Marshall Islands, and the star chart rafters of the Kiribati maneaba.

Symbols and divination
The oracle bone and tortoise shell inscriptions of the Neolithic period to Shang dynasty Dongyi people of Shandong and neighboring provinces used symbols that had no obvious graphic realism.
Some of the glyphs could plausibly relate to figures made of string, stick, rings, etc. hanging from cords as mnemonic devices used in early record and story-keeping.

Oracle bone and tortoise shell glyphs from http://www.paulnoll.com/China/Culture/language-oracle-bone.html with the top row showing simple glyphs, the middle row more advanced composite glyphs, and the bottom, complex composite glyphs. The top row glyphs have some resemblance to present-day Chinese knot wall hangings, and may have represented string figures hanging from larger recording cords.
Knots, symbols and similar devices served the same purposes as scripts later on, to include record-keeping, story-telling, aiding instruction and even use for personal communication.
Regards,
Paul Kekai Manansala
Sacramento
References
Cajori, Florian. A History of Mathematical Notations/Two Volumes Bound As One/Notations in Elementary Mathematics,..., Courier Dover Publications, 1993.
Day, Cyrus L. The Role of the Knot in Primitive Ancient Cultures, Lawrence: University of Kansas Press, 1967.
Kanahele, George Hu'eu. Ku Kanaka Stand Tall: A Search for Hawaiian Values University of Hawaii Press, 1993, p. 285.
Manansala, Paul. "Sungka Mathematics of the Philippines," Indian Journal of History of Science 30(1), New Delhi: Indian National Science Academy, 1995.
Przyluski, Jean. Pre-Aryan and Pre-Dravidian in India, Calcutta: University of Calcutta, 1929.







0 comments:
Post a Comment